Page 123 - ALL_Рени-Дамянова-Тяло-Финал-1-280_Content_links

- решенията на експертите са класирани (допуснати) или некласирани (отхвърлени)
резултати от теста.
При това се тръгва от основното предположение, че стойностите на променливата вели-
чина – действителни учебни постижения и компетентност на успелите при тестирането лица,
τ i е най-малко равна или по-висока от поставения стандарт за успешност τ z, т.е. τ i ≥ τ z. Тъй
като, независимо дали тестовете са нормативни или критериално-ориентирани, действител-
ните учебни постижения са латентен признак, дефинират се от стойностите на наблюдаваните
балове (Х) и може да се опишат чрез функцията f (Х, τ).
В теорията на критериално-ориентираните тестове са известни няколко математически мо-
дела за оценка на рисковете от грешни решения – функция на загубите, основана на граничните
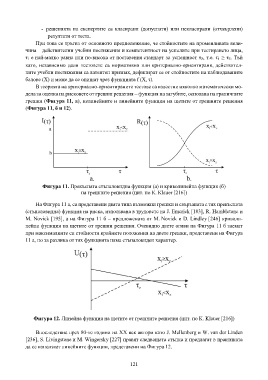
грешки (Фигура 11, а), нелинейните и линейните функции на щетите от грешните решения
(Фигура 11, б и 12).

Фигура 11. Прекъсната стъпаловидна функция (а) и криволинейна функция (б)
на грешните решения (цит. по К. Кlauer [216])

На Фигура 11 а, са представени двата типа възможни грешки и свързаната с тях прекъсната
(стъпаловидна) функция на риска, използвана в трудовете на J. Emerick [183], R. Hambletone и
М. Novick [195], а на Фигура 11 б – предложената от М. Novick и D. Lindley [246] криволи-
нейна функция на щетите от грешни решения. Очевидно двете огиви на Фигура 11 б заемат
при максималните си стойности крайните положения на двете грешки, представени на Фигура
11 а, но за разлика от тях функцията няма стъпаловиден характер.

Фигура 12. Линейна функция на щетите от грешните решения (цит. по К. Klauer [216])

Впоследствие през 80-те години на XX век автори като J. Mellenberg и W. van der Linden
[236], S. Livingstone и М. Wingersky [227] правят следващата стъпка и предлагат в практиката
да се използват линейните функции, представени на Фигура 12.

121