Page 131 - ALL_Рени-Дамянова-Тяло-Финал-1-280_Content_links

произтича и основното предимство на теорията на положителния отговор спрямо класическата
теория на тестовете, изразяващо се в преодоляване на липсата на инвариантност на класичес-
кия модел на дидактическите тестове. С други думи, параметрите на тестовите задачи, изчис-
лени с моделите от теорията на положителния отговор, са инвариантни при смяна на извад-
ките, върху които се прилагат дидактическите тестове.
Приложението на различните модели, участващи в теорията на положителния отговор,
изисква изчерпателна проверка на 4-те основни предположения, върху които са изградени: ед-
номерност, равни индекси на дискриминация, минимално налучкване, нормална времева про-
дължителност на провеждане на теста (т.е. тестът да не е скоростен).
Информационната функция на теста (нар. Test Information Function – TIF), представляваща
мярка за точността на оценката на получените балове в основите на теорията на положителния
отговор, е своеобразен аналог на надеждността и стандартната грешка на измерването от
класическата теория на тестовете.
Както характеристичната, така и информационната функция на един тест се получават
след изчисляване на трудността и дискриминацията на всяка тестова задача, включена в него.
И двете функции зависят от характеристиките на отделните задачи, както и от използваните
модели – еднопараметичен или двупараметричен.
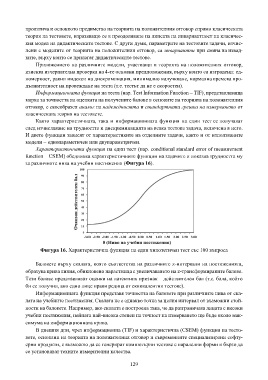
Характеристичната функция на един тест (нар. conditional standard error of measurement
function – CSEM) обединява характеристичните функции на задачите и показва трудността му
за различните нива на учебни постижения (Фигура 16).

Фигура 16. Характеристична функция на един хипотетичен тест със 100 въпроса

Баловете върху скалата, която съответства на различните z-интервали на постиженията,
образува крива линия, обикновено нарастваща с увеличаването на z-трансформираните балове.
Тези балове представляват оценки на латентния признак – действителен бал (т.е. бала, който
би се получил, ако едно лице прави редица от еквивалентни тестове).
Информационната функция представя точността на баловете при различните нива от ска-
лата на учебните постижения. Скалата не е еднакво точна за целия интервал от възможни стой-
ности на баловете. Например, ако скалата е построена така, че да разграничава лицата с високи
учебни постижения, нейната най-висока степен на точност на измерването ще бъде около мак-
симума на информационната крива.
В днешни дни, чрез информационна (TIF) и характеристична (CSEM) функция на тесто-
вете, основани на теорията на положителния отговор и съвременните специализирани софту-
ерни продукти, е възможно да се генерират компютърни тестове с паралелни форми и бързо да
се установяват техните измерителни качества.

129